Alpha 101

原文：101 Formulaic Alphas By Zura KaKushadze

摘要

我们提供了101个真实的量化交易alpha的显式公式，这些公式也可以转化为计算机代码。
它们的平均持有期大约在0.6到6.4天之间。这些alpha之间的平均成对相关性较低，为15.9%。
这些回报与波动率强相关，但对换手率没有显著依赖，直接证实了一个基于更间接的经验分析的早期结果。
我们进一步发现经验上换手率对alpha之间的相关性解释能力较差。

引言

在现代量化交易中存在两种互补的趋势，而且在某种意义上甚至是相互竞争的。一方面，越来越多的市场参与者（例如，量化交易员等）利用复杂的量化技术挖掘alpha。这导致了越来越模糊和短暂的alpha出现。另一方面，技术进步使得基本上可以自动化（大部分）alpha收获过程。这带来了越来越多的alpha，其数量可能达到数十万甚至数百万，随着这一领域的指数级增长，这一数量在我们知道之前可能会达到数十亿。

这种alpha的大量增加，尽管大部分是模糊和短暂的，但允许以复杂的方式将它们组合起来，形成一个统一的“超级alpha”。然后实际上交易的是这个“超级alpha” —— 而不是交易个别的alpha —— 这还带来了自动内部交易的额外好处（从而在交易成本等方面实现了关键的盈利性节省），alpha投资组合的多样化（这可以对冲任何给定时间段内的任何alpha子集的破产），等等。在组合alpha时面临的挑战之一是通常的“变量过多，观察不足”的困境。因此，alpha样本协方差矩阵严重奇异。

此外，量化交易是一个神秘的领域，从业者的数据和其他信息并不容易获得。这无意中在现代量化交易周围形成了一个谜团。例如，有这么多的alpha，它们不是高度相关吗？这些alpha是什么样的？它们主要是基于价格和成交量数据，均值回归，动量等吗？alpha的回报如何取决于波动率、换手率等？

在之前的一篇论文中[Kakushadze和Tulchinsky，2015]通过研究4000个真实生活中的alpha的一些经验性质，对现代量化交易领域进行了一步解密。在本文中，我们迈出了另一步，提供了101个真实量化交易alpha的显式公式，这些公式也可以转化为计算机代码。我们的公式化alpha，尽管大多数不一定都那么“简单”，但其目的在于让读者一窥一些较为简单的真实生活中的alpha是什么样子。这也使读者能够在历史数据上复制和测试这些alpha，并进行新的研究和其他经验分析。希望这进一步激发（年轻）研究者提出新的想法，并创造出他们自己的alpha。

我们在第2节讨论了我们的公式化alpha的一些一般特征。这些alpha大多是基于“价格-成交量”（日收盘-日收盘回报、开盘价、收盘价、最高价、最低价、成交量和成交量加权平均价）的，尽管一些alpha中使用了“基本面”输入，其中包括一个利用市值的alpha，以及一些利用一种二进制行业分类（如GICS、BICS、NAICS、SIC等）的alpha，这些分类用于对各种数量进行行业中性化处理。

在第3节中，我们根据个别alpha的夏普比率、换手率和每股收益数据，以及一个样本协方差矩阵，讨论了我们的alpha的经验性质。平均持有期大约在0.6到6.4天之间。这些alpha之间的平均（中位数）成对相关性较低，为15.9%（14.3%）。回报与波动率强相关，就像[Kakushadze和Tulchinsky，2015]中一样，我们发现了一个经验性的比例关系。

$$R = V^X$$

对于我们的 alpha 101，$X = 0.67$。此外，我们发现这些alpha的回报与换手率之间没有显著的依赖关系。这直接证实了[Kakushadze和Tulchinsky，2015]的一个早期结果，该结果是基于更间接的经验分析得出的。

我们进一步通过经验发现，换手率本身对alpha之间的相关性的解释能力较差。这并不意味着换手率在诸如通过因子模型对协方差矩阵建模等方面没有价值。

我们在第4节中简要总结。附录A包含我们的公式化alpha以及其中使用的函数、运算符和输入数据的定义。附录B包含一些法律术语。

公式化 Alpha

在本节中，我们描述了我们101个公式化alpha的一些一般特征。这些alpha是WorldQuant LLC所有，并且在此处使用是经过其明确许可的。在alpha的专有性质的限制下，我们尽可能提供了尽可能多的细节。公式表达式，也就是计算机代码，已经给出在附录A中。

粗略地说，可以将alpha信号视为基于均值回归或动量。均值回归alpha的符号与其基于的回报相反。例如，一个简单的均值回归alpha可以表示为:

$$-ln(\text{today’s open} / \text{yesterday’s close})$$

这里的昨日收盘价已经调整了任何拆分和股息，如果除权日是今天的话。这里的想法（或希望）是股票会均值回归，并且会部分回归到之前的收益（如果今天的开盘价高于昨天的收盘价），或者部分弥补之前的损失（如果今天的开盘价低于昨天的收盘价）。这是所谓的“延迟0” alpha。通常，“延迟0”表示在alpha中使用的一些数据（例如价格）的时间与预期进行交易的时间重合。例如，alpha（2）最好在今天的开盘价或更现实地说，尽可能接近今天的开盘价时进行交易。更广泛地说，这个时间可能是其他时间，例如收盘价。

一个简单的动量alpha的例子如下：

$$ln(\text{yesterday’s close} / \text{yesterday’s open})$$

在这种情况下，价格是否调整没有影响。这里的想法（或希望）是，如果股票昨天上涨（下滑），则趋势将在今天继续，收益（损失）将进一步增加。如果意图是今天进行交易（例如，从开盘开始），则这是所谓的“延迟1” alpha。通常，“延迟1”表示alpha在计算中使用的最新数据的日期之后的第二天进行交易。类似地，“延迟􏰒” alpha的定义也相同，其中􏰒表示使用的数据离样本外的天数。

在复杂的alpha中，均值回归和动量的元素可以混合在一起，使它们在这方面不那么明显。然而，可以将这些alpha的较小的构建块视为基于均值回归或动量的。例如，附录A中的Alpha#101是一个延迟1的动量alpha：如果股票在盘中上涨（即，收盘价>开盘价且最高价>最低价），则第二天可以在该股票中建立多头头寸。另一方面，附录A中的Alpha#42本质上是一个延迟0的均值回归alpha：如果股票在第二半天内上涨（收盘价>成交量加权平均价），则排名（成交量加权平均价 - 收盘价）较低，相反如果股票下跌（收盘价<成交量加权平均价）。分母将权重降低。“反向”头寸是在接近收盘时建立的。

数据和alpha的经验性质

在本节中，我们基于WorldQuant LLC所有的数据描述我们公式化alpha的经验性质，这些数据在此处经过了其明确许可的使用。在这个数据集的专有性质的限制下，我们尽可能提供尽可能多的细节。

对于我们的 Alpha，我们定义年化日夏普比 $S$，日换手率 $T$，每股的美分价格 $C$。现在我们把 Alpha 用 $i$ ($i = 1, …, N$) 标记，其中 $N = 101$ 就是我们 Alpha 的总量。对于每一个 Alpha，$S_i, T_i, C_i$ 定义如下：

$$S_i = \sqrt{252}\frac{P_i}{V_i}$$

$$T_i = \frac{D_i}{I_i}$$

$$C_i = 100 * \frac{P_i}{Q_i}$$

其中， $P_i$ 是平均如 Pnl （美金计量）；$V_i$ 是日投资组合波动率；$Q_i$ 是平均每日交易的股票数量；$D_i$ 是平均每日美金交易量；$I_i$ 是该 Alpha 投资的总美元数量。更准确的说，$I_i$ 的本金部分是恒定的，但是它会随着每天PNL而浮动。所以在计算 $S_i$ 的时候，$D_i$ 和 $I_i$ 都会调整以确保 I 是恒定的（没看懂）。
本文收集数据的时间跨度为 2010-01-04 到 2013-12-31 。我们计算了该期间 alpha 日回报率的协方差矩阵 $\gamma {ij}$，总样本数为 1006，$\gamma{ij}$ 是非奇异的。这样，日波动率就是 $\sigma^2 = \gamma_{ij}$，而相关矩阵 $\Psi_{ij} = \gamma_{ij} / \sigma_i\sigma_j$ （$\Psi_{ii}=1$）。注意，$V_i=\sigma_iI_i$，而日平均回报率 $R_i=P_i / I_i$。

表1 和 图1 总结了年化夏普率、日换手率、持仓周期、美分每股、日回报波动率、年化平均收益以及 $N(N-1) / 2$ 个相关系数 $\Psi_{ij}$，其中 $i > j$。

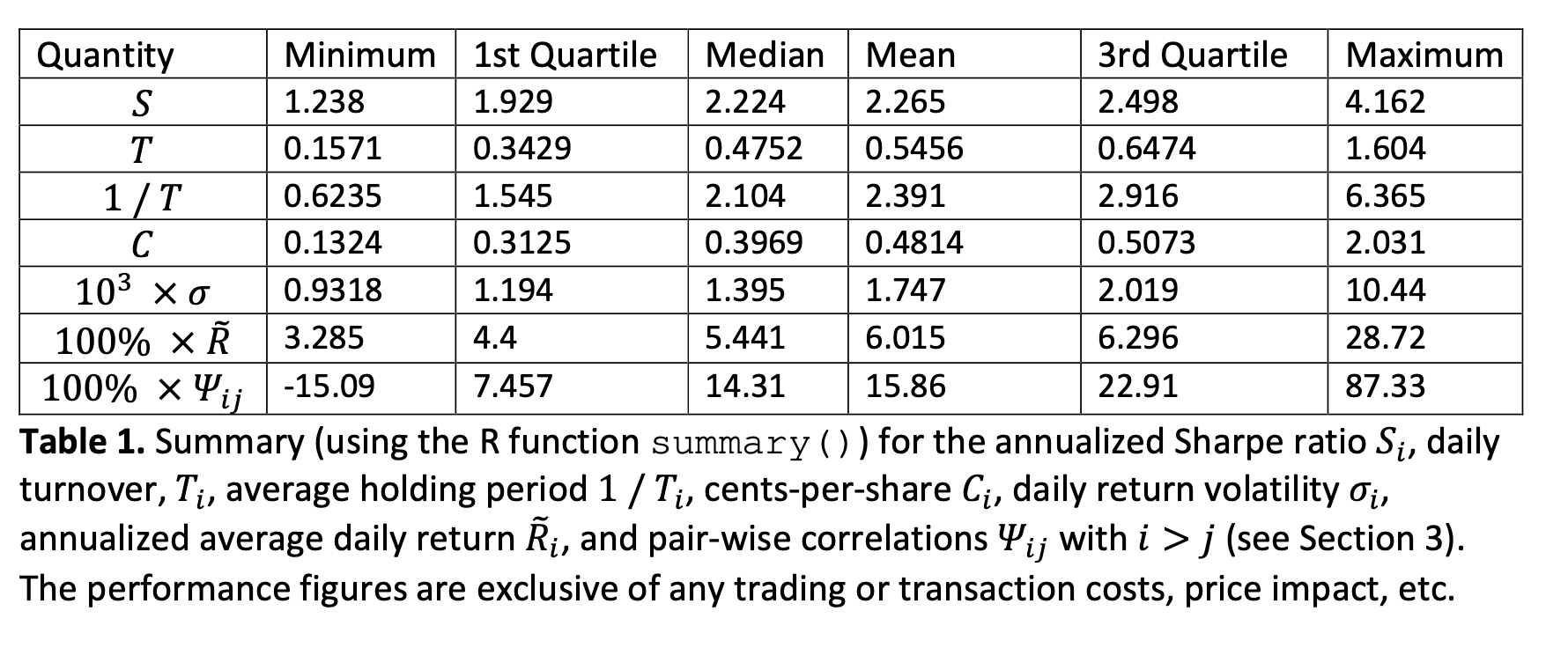
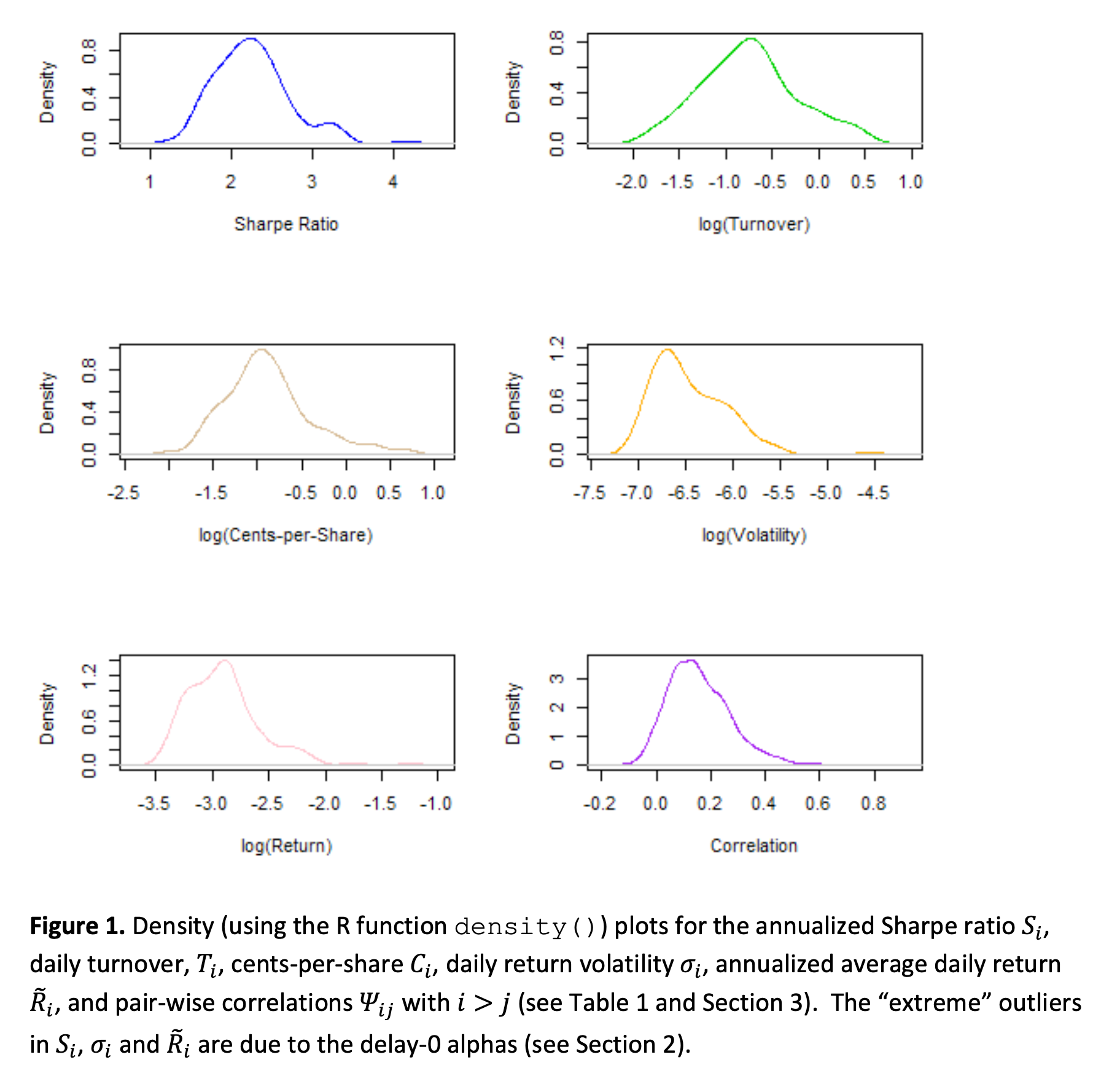
回报率、波动率和换手率

与[Kakushadze和Tulchinsky，2015]一致，我们发现换手率与alpha之间没有统计上显著的依赖关系，而平均每日回报与每日回报波动率强相关。

换手率可以解释相关性吗？

如果我们将alpha与股票进行类比，那么alpha的换手率类似于股票流动性，通常通过平均每日交易额（ADDV）来衡量。ADDV的对数通常被用作多因子风险模型中的风格风险因子，用于近似股票投资组合协方差矩阵的结构，其主要目标是建模协方差矩阵的非对角元素，也就是成对相关性结构。按照这个类比，我们可以问一下换手率 - 或者更准确地说它的对数 - 是否对建模alpha之间的相关性有解释能力。显然，直接使用换手率（而不是其对数）是无济于事的，因为换手率分布高度偏斜（大致呈对数正态分布）（参见图1）。

让我们强调一下，我们的结论并不一定意味着换手率在因子模型环境中没有增加价值，它只是意味着换手率本身似乎不利于建模成对alpha之间的相关性。上述分析并未解决换手率是否增加了建模方差（例如，特异风险）的解释价值的问题。因此，对ln(􏰚)对ln(􏰈)进行线性回归（包括截距）显示了这些变量之间的非零相关性（见表5），尽管不是非常强。要查看换手率是否通过特异风险增加价值，需要使用某些专有方法，超出了本文的范围。

结论

我们强调，我们在这里提供的101个alpha不是“玩具”alpha，而是真实的用于生产的交易alpha。事实上，截至本文撰写时，其中80个alpha正在生产中使用。据我们所知，这是文献中首次出现如此大量真实的显式公式alpha。这应该不足为奇：自然而言，量化交易是高度专有和保密的。我们在这里的目标是提供一瞥现代量化交易复杂且不断发展的世界，并帮助尽可能解密它。

如今的技术进步使得量化交易alpha的挖掘自动化成为可能。量化交易alpha是可转化为交易策略/组合的可用交易信号中数量最多的。在一个（美元中性的）投资组合中，例如最流动的2000只美国股票的个别股票持仓有无数的排列组合可能会在高频和中频时间跨度上产生正回报。此外，许多这些alpha是短暂的，它们的范围是非常流动的。要挖掘数十万、数百万甚至数十亿的alpha，并将它们合并为统一的“超级alpha”，需要具有量化分析技能、技术设备齐全并不断适应的交易操作。这样的超级alpha可以通过自动交易内部交叉获得可观的执行成本节省。

在这种精神下，我们以俄罗斯诗人米哈伊尔·列尔蒙托夫（Mikhail Lermontov）的一首1832年的诗结束这篇文章。以下是由祖拉·卡库沙泽（Zura Kakushadze）翻译的诗歌（约1993年）：

帆

一帆孤影白如霜，
在蓝色大海的雾中，
外来的狂风在寻觅力量，
为何逃离了家乡的港湾？

帆杆在弯曲中发出嘎吱声，
风浪前行，狂风怒涛，
它不是在寻找幸福，
也不是逃离幸福！

下面是湛蓝的海流奔腾，
上面是闪耀的金色光芒，
但帆似乎渴望着风暴，
仿佛在风暴中寻找平静。