0.1 比特币的基础组成模块
Info
【比特币】最重要的基础模块之一是数字签名
- 中本聪
人们开始使用这些基础模块进行思考,而不是(组成这些模块的)更小的部分思考。最后,模块(在整体中)慢慢都溶解了,留下了一种关系,而这些关系重复他们自己,并未【整体】提供结构。
- Christopher Alexander
如果不讨论组成比特币的各个基础模块的话,没人可以解释清楚比特币是什么。因此,虽然公钥密码学、数字签名、散列函数和对等网络并不是在热闹的鸡尾酒会上最先出现的话题(译者按:非常英语的玩笑话,就是说这些话题普通人不会谈论),但一旦充分理解这些深奥的结构,这些东西就开始变得非常有魅力。
尽管我不打算深入探讨这些概念的数学原理,但我相信详细了解总体思路会有所帮助。虽然不是每个人都需要了解椭圆曲线密码学的来龙去脉,但如果您想正确使用比特币,则需要了解某些事项。例如,如果您要获得比特币的所有权,您将需要了解什么是私钥——这将我们带到比特币的第一个基本构建块:公私密钥对。
公钥密码学
公钥密码学,也被称作非对称密码学,是所有现代加密协议的核心,包括比特币。正如 James Dale 在 《The Sovereign Individual》中提到的,这些数学”小技巧“导致了我们世界权力动态的根本转变。
公钥密码学的基本原理是这样的:根据一个秘密字符串(译者按:你自己随机挑选的),你会得到一对秘钥:一个公开的(公钥),一个秘密的(私钥)。这些秘钥是不对称的,换句话说,你用其中一个锁门,用另一个开门。
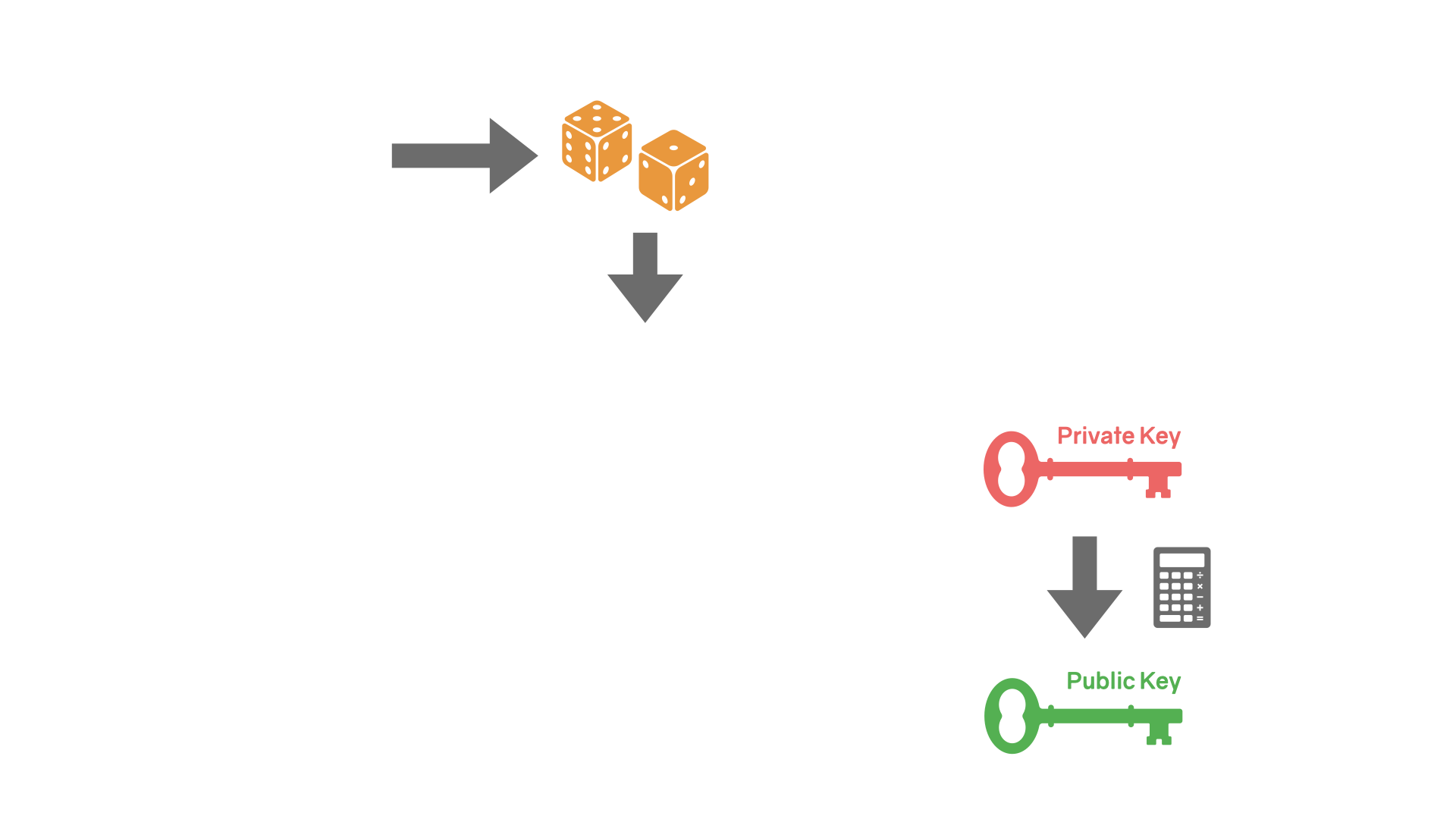
当然,这些秘钥并不是实体的钥匙,我们说的也不是真实的门。这些秘钥是数据,而门是算法,锁门的意思是加密(把数据编程噪声),开门就是解密(把噪音还原成数据)。被加密的信息,或者在比特币的下上文里面被称作签名,也是数据。
现代密码学系统都是透明系统。换句话说,即使黑客知道系统的每一个实现细节,只要他们不知道你的私钥,系统就是安全的1。比特币就是这样一种透明系统,虽然比特币没有加密任何数据。在密码学术语里,比特币利用了两个技术:密码学散列和数字签名,这两个技术都与加密不同。比特币没有秘密。唯一的秘密属于你:你的私钥。只要你保证私钥的安全,你的比特币就是安全的。
总结一下:我们用公钥密码学来床在两个数学上相互关联的数字。一个公开的数字,是公钥;另一个是秘密的。那个秘密的数字就是私钥,而公开的数字是公钥。比特币是使用上面两个秘钥的一个现代的密码学系统。
数字签名
签名之所以有用是因为它写起来很快,可以验证并且难以被复制。签署一份文件往往意味着签字的主人已经阅读并、理解并且同意了这份文件。签名不仅可以验证文件——确保文件在事后没有被更改——还可以验证签名者。
在比特和字节的世界中,由于公钥密码学,数字签名也可以实现同样的目的。
数字签名是可应用于数据的特殊数学函数的结果。一个用户,我们称她为爱丽丝,可以使用她的私钥签署任意消息,而其他用户——实际上每个人——都可以使用爱丽丝的公钥来验证她,而且只有她,创建了那个签名。
适当的数字签名方案可确保:
- 数据完整性。即数据在签名后没有被篡改
- 授权性。确保是签名人签署了文件
- 不可否认性。签名人不能否认签署
换句话说,对消息进行数字签名将发送者的身份绑定到消息本身,就像常规签名将人绑定到文档一样。然而,由于密码学,数字签名带来的保证比物理签名的保证更强大。伪造由强签名方案创建的数字签名几乎是不可能的。除了这些强大的完整性和身份验证保证外,数字签名还易于创建和验证。
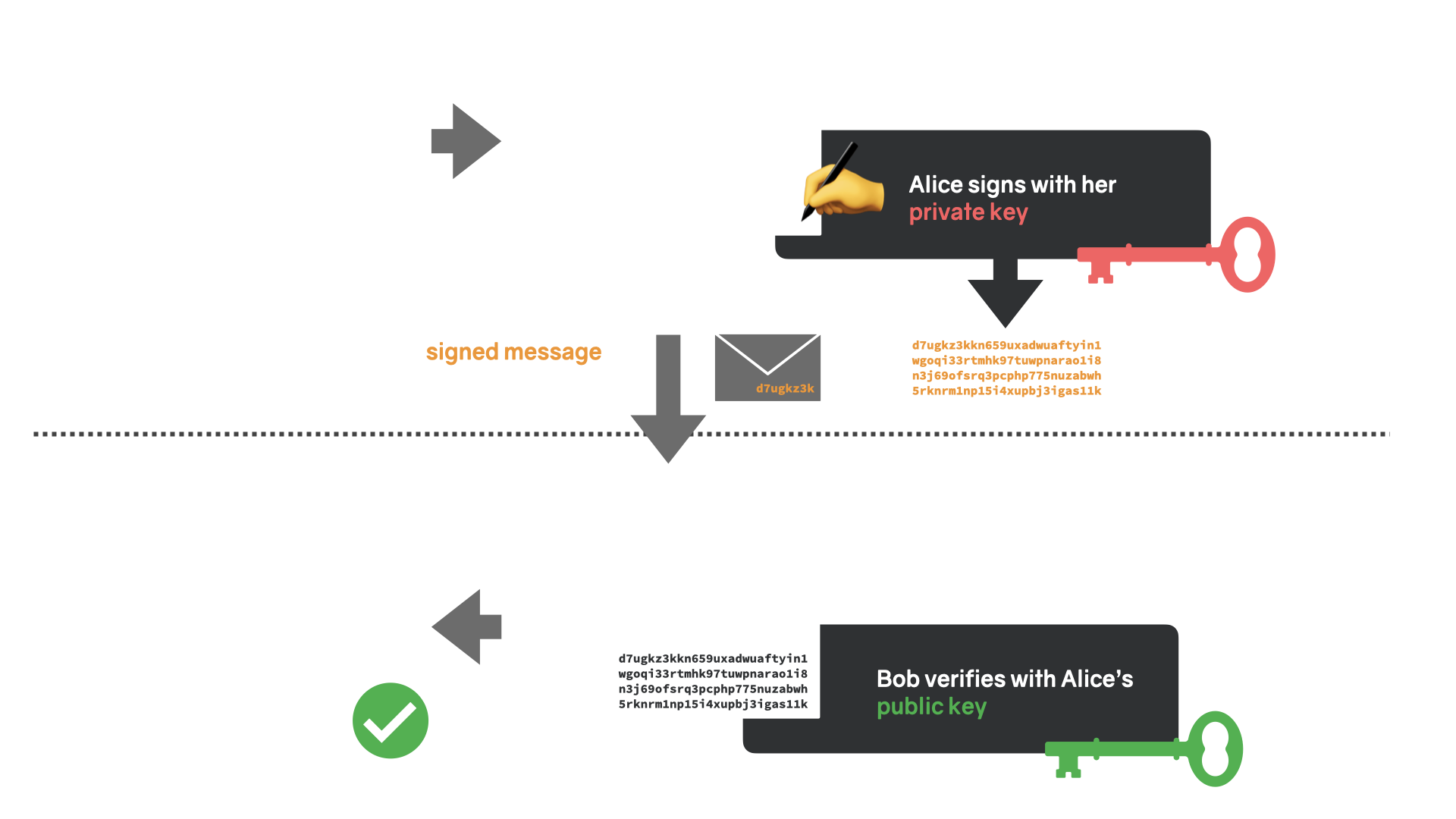
总结一下:数字签名用于验证消息是否由已知发件人创建并且消息在传输过程中未被更改。
在比特币中,数字签名用于签署交易。只有有效的交易才会被散列并打包到一个块中,并且只有有效的块才会被散列,以便它们可以添加到现有的块链中。这将我们带到下一个构建块:哈希函数(散列函数)。
散列函数
散列函数是一种单向函数,它接受任意长度的输入并计算具有固定长度的“指纹”。散列函数也称为“单向门”函数,因为它很容易掉进单向门,但又不可能再出来。类似地,很容易计算一段数据的哈希值,但不可能仅从该哈希值计算出所述数据的原始内容。
$ echo "Satoshi Nakamoto" | sha256sum
2662d47e3d692fe8c2cdb70b907ebb12b216a9d9ca5110dd336d12e7bf86073b
反向计算是不可能的,因为有效输入的空间远远大于可能输出的空间,这意味着,从本质上讲,在计算哈希时信息会丢失。
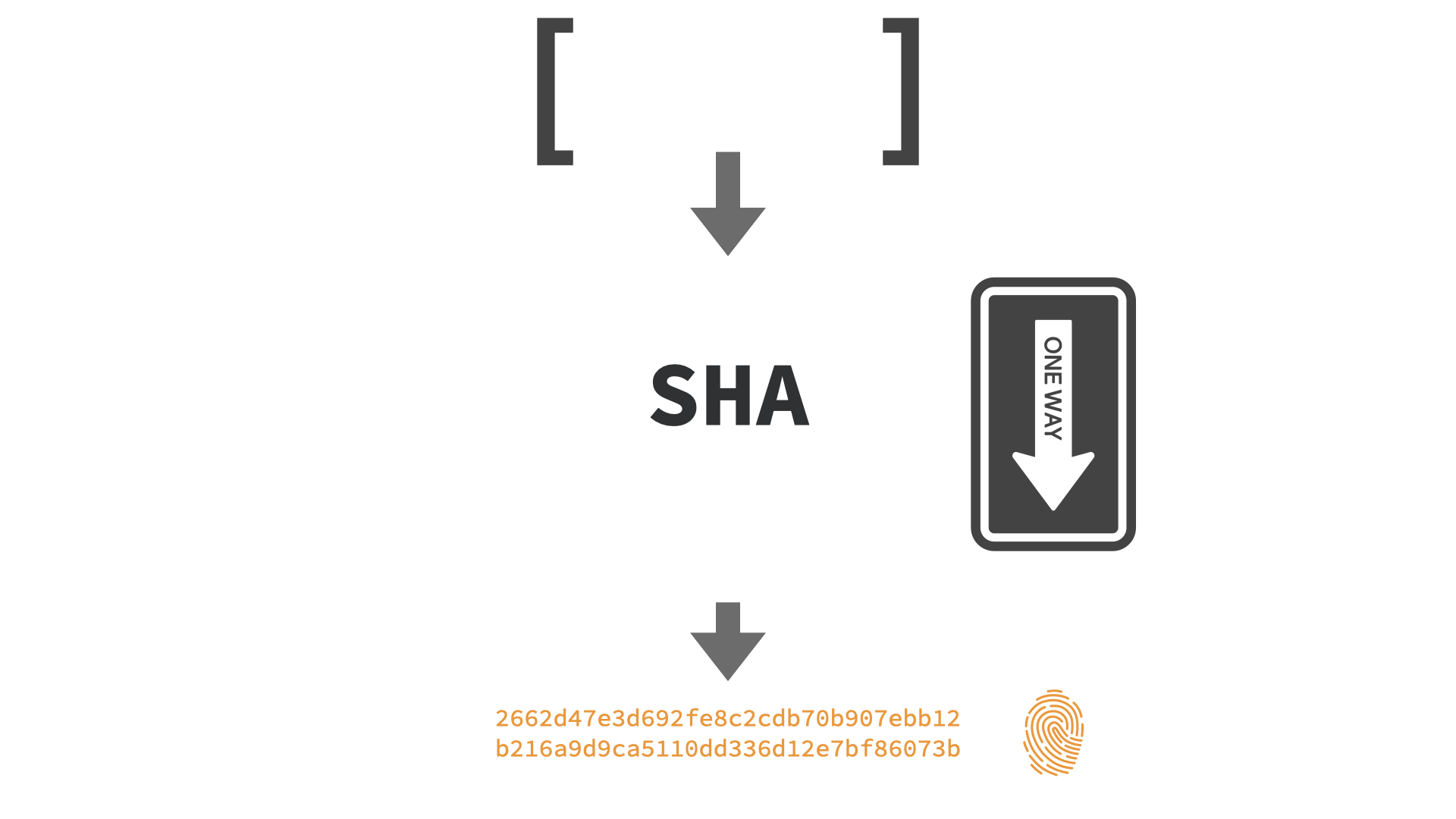
因此,两个不同的数据可以具有相同的哈希值。这就是我们所说的哈希碰撞。常规哈希函数和加密哈希函数之间的区别在于输入数据如何映射到可能的哈希空间。密码哈希函数具有某些属性,可确保不可能发现冲突,即产生相同输出的两个输入。此外,加密散列函数可确保稍微不同的输入会产生截然不同的输出等。
散列函数在比特币协议中随处可见。比如,我们说的挖矿就是找到一个数字是的当前区块的散列值满足某个条件。比特币协议使用的散列算法是 SHA256 函数。比特币地址的生成也是用了散列函数(不是 SHA256),识别赎回脚本、交易记录、区块等等都用到散列函数。
哈希函数是一个如此重要的构建块,因为没有中央权威,数据本身就是我们识别和索引信息的全部。我们无法查找将所有数据整齐地组织起来的中央索引或寄存器,因为不存在这样的权威。这将我们带到了最后一个构建块:对等网络。
对等网络
常规计算机网络的问题是一个政治问题。传统的计算机网络通常采用客户端-服务器模型,即由一台服务器作为网络的中央管理机构。不幸的是,正如我们过去所见,服务器并不总是为其客户端服务。通常情况下,服务器会转变为独裁者,这就是为什么使用术语“主人”而不是“服务器”并且不谈论“客户”而谈论奴隶同样公平。
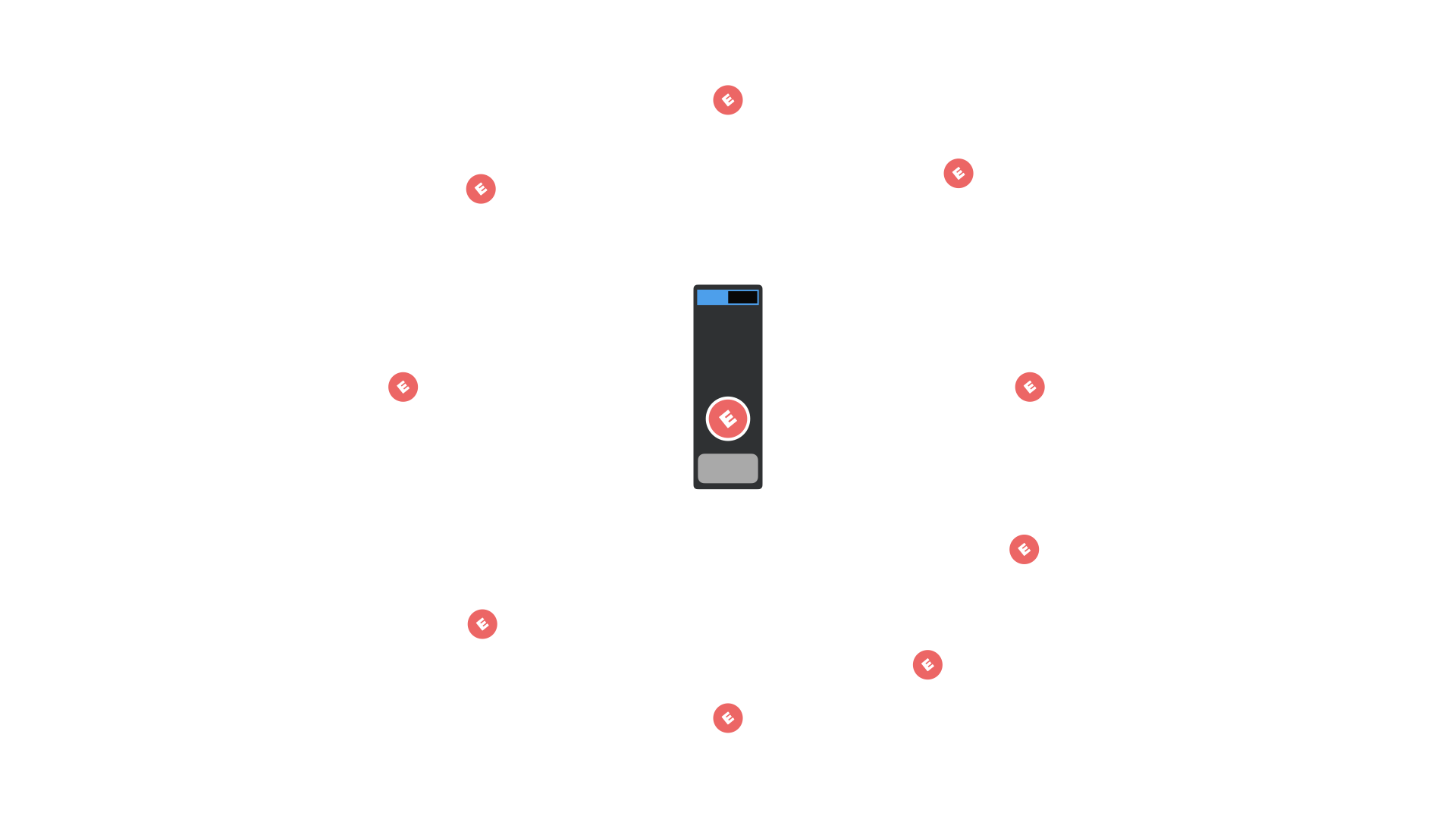
解决这个难题的方法是通过设计让网络中的每个人都成为平等的参与者。我们在网络中有节点,而不是主节点和从节点。平等的参与者不仅享有同等的特权,更重要的是,他们的权力是平等的。
比特币网络是一个对等网络。这一点对于比特币网络尤其重要。我认为,这是一个必须要坚持的特征。如果坚持这个特征,就一定会出某个中心,而中心会弥散开来渐渐控制整个网络。历史已经证明,中央集权会带来难以抗拒的权利。然后,任何中央机构都会开始乱用权利,这也是比特币维持去中心化的原因。
放在一起!
正如我们将在第 1 章中看到的,许多人认为应该可以使用这些构建块设计一个数字货币系统。事实证明他们是对的,但是中本聪的天才使这一切成为现实。
比特币的工作方式真的是一个迷。之前说的这些基础跟博弈论产生了微妙的连接,碰撞出了一个不同于以往的自调节系统。
而且,正如我们刚才提到的,描述这个系统的语言不是特别准确。比如私钥、公钥、地址、钱包、币、交易等等,这些东西其实都仅仅是”数据“,而不是我们印象中的实体。使用这些语言容易在脑海中形成有所偏差的模型。
然而,我也只能做到这样了。毕竟语言和比喻是我们理解事物的主要工具。所以,之后我也会用更多的比喻。
假设您的钱包里有一些 sats,想将 615 sats 发送给 Alice。你可以认为你所要做的就是打开你的钱包,取出 615 sats,然后将它们发送给 Alice,就像电子邮件的附件一样。
然而,事实并非如此。。。完全不是。。。
首先,你”拥有“的 Sats 不在所谓的钱包里,它们都在一个透明的罐子里,所有人都能看到它们。你的钱包其实是打开金库的钥匙,当你将 615 Sat 发送给 Alice 的时候,你解锁了你的保险库,并且把一部分安上了 Alice 的锁。现在只有 Alice 的私钥可以打开这把锁了。如果 Alice 想要花这 615 Sats,你需要打开锁,然后加上其他人的锁。(译者按:如果你把你的 Sat 加上了其他人的锁,你就”失去“对这部分 Sat 的控制了)。
但是,那不是把我所有的资金都转移给爱丽丝了吗?没错,这就是每次交易都会创建新保险库的原因。在这种情况下,一张给爱丽丝,一张给你拿回零钱。还有两个细节:
- 你的钥匙不是真的钥匙,仅仅是一个说法。
- 不在保险柜里面的 Sat 是不存在的。
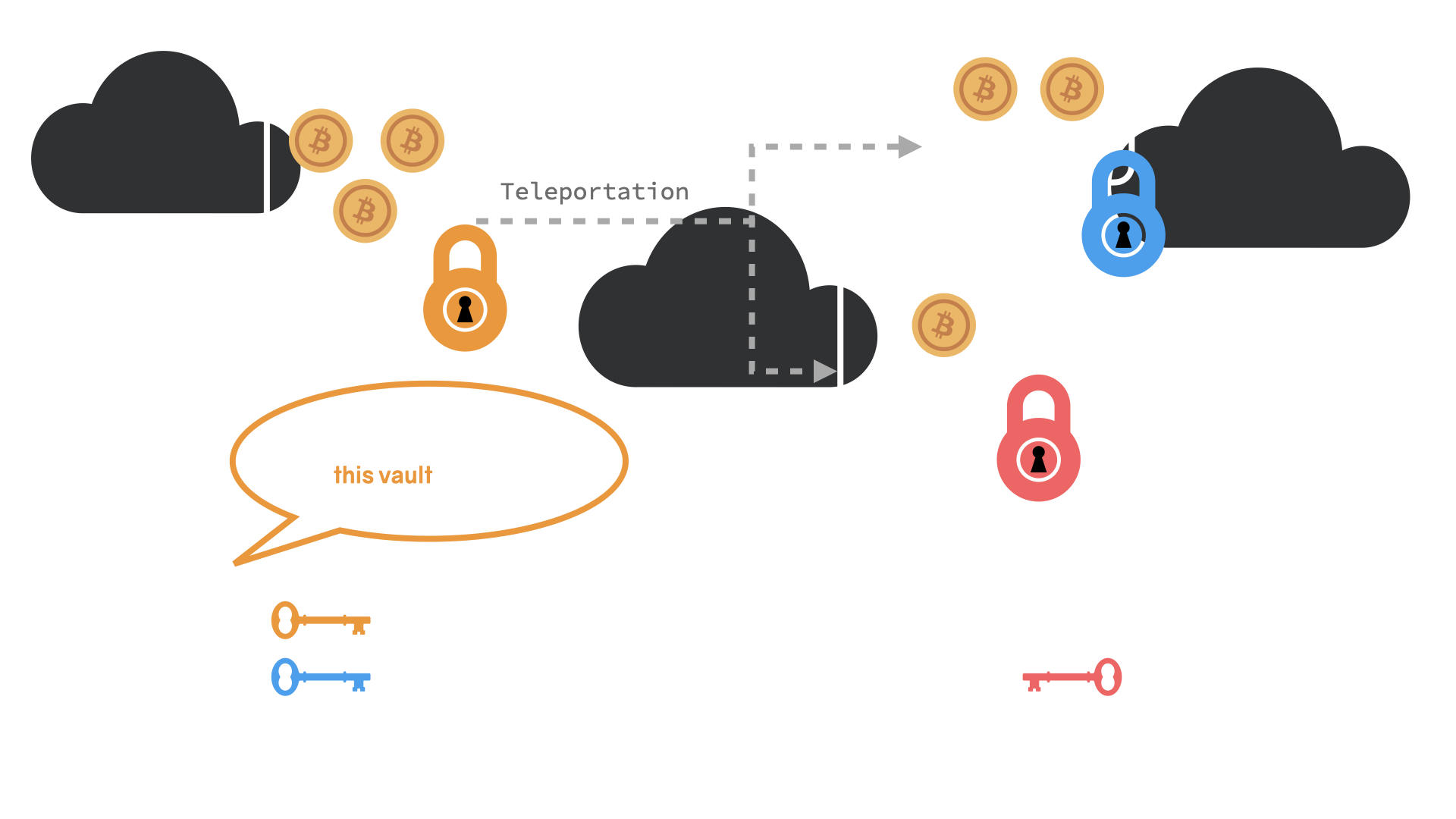
用比特币的语言重述上面的过程:要发起资金转移,Alice 需要用他的私钥签名这笔交易。这笔交易的输出之一是 Bob,地址源自 Bob 的公钥(注意不是他的公钥)。一旦带着 Alice 签名的交易记录被广播到比特币网络,所有收到这条交易的节点都会检查这条交易是否符合规则,如果合法且被确认,交易就完成了。Alice 的旧保鲜库空了,但是两个新的保险库出现了:一个是 Alice 的,一个是 Bob 的。(这些保险库在比特币世界中被叫做 UTXO)
虽然这个图像也不是完整的,但是他对 Sat 的转移做了比较精确的描述。我希望随着这本书的深入,你对比特币的图像产生更加清晰的认识。好了,在我们进一步理解比特币之前,我们来看看比特币的历史。(译者按:很好的思路。)
-
This is known as Kerckhoff's principle or Shannon's maxim. It is the opposite of "security through obscurity." ↩